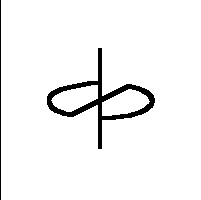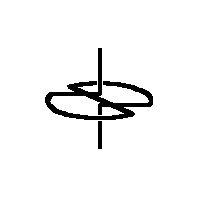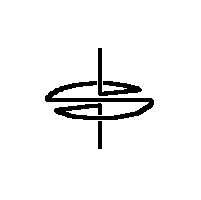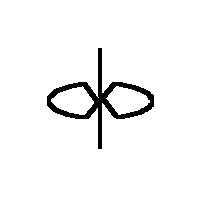This article was published in the newsletter no. 34 (1996) of GIREP (Groupe International de Recherche sur l'Enseignement de la Physique)

The paper-clip top (Sakai-top)            

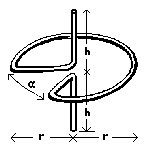
Principal construction

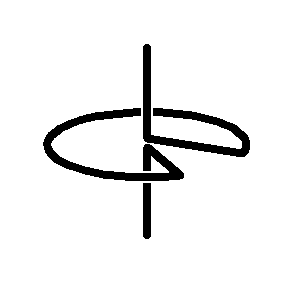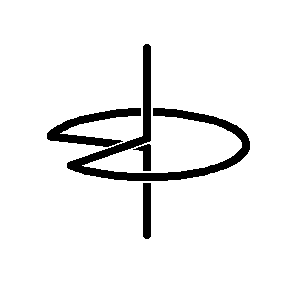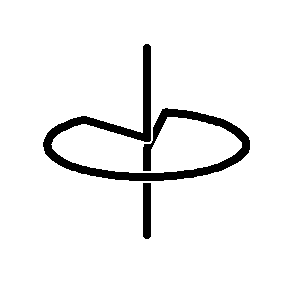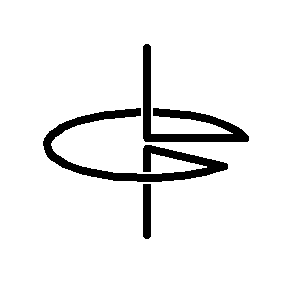The first Sakai Top (an unsymmetrical top) an animation

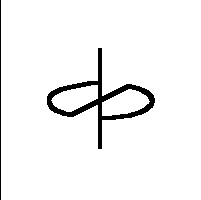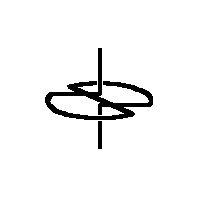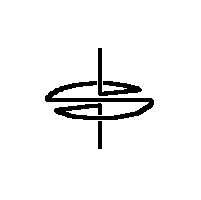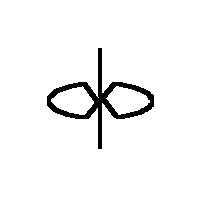
A second Sakai Top (a symmetrical top) an animation

Video of a real Sakai Top Thanks to Dr. J. Yingprayoon/Thailand

Video of a real Sakai Top download Sakai_Top.avi (AVI-file; 3.2MB)

High-speed-video of a Sakai Top download Sakai1_1000fps.mp4 (mp4-file; 1000fps; 115kB)

You can bend a top out of one piece of wire, e.g. a paper-clip. Takao Sakai, professor of mechanical engineering at the Fukushima Technology Centre in Kohriyama-City in Japan has proposed an ingeniously simple solution. His top consists of a sector of a circle, from which the spokes lead to the shaft (= rotating axis) and in this way hold the arc of the circle. The spokes form an angle alpha. Both ends of the wire form the shaft - bent rectangular to the spokes in the center of the circle. The top will only work properly if the center of gravity of the whole system stays in the axis. This is exactly the case if tan(alpha/2) = 1/2, with alpha being the angle between the spokes. It is a nice exercise for physics students to prove that. The angle alpha = 53.13 degrees. To actually build the top you need a small pair of pliers and a metal paper-clip. Since it is not possible to bend the wire sharply, although the angle alpha was calculated under this condition, you may bend the angle a a little smaller than 53 degrees. Using regular paper-clips, the height h and the radius r of the circle are only about 1cm. The Sakai-top runs well even if the curvature of the circle is not perfect. You can see the circle and the shaft of a very well made and fast rotating top distinctly, while the spokes will be almost invisible. If you spin it with your fingers, the small diameter of the wire will make the top rotate very fast, up to several thousand r.p.m. Try to calculate roughly the revolutions under your personal conditions (finger velocity and diameter of the wire) and then to measure the revolutions per minute with a stroboscope. Be careful not to use all the paper-clips in your surroundings. A recommendable book by Wolfgang Bürger (in German) about physics toys and related reflections has recently appeared: Der paradoxe Eierbecher, Birkhäuser-Verlag, Basel 1995. There you can find some more information about the Sakai-top.